Part 4 - Calculating BER

Objectives

You will use the BER values recorded for the baseband communication systems (both uni- and bipolar) to plot the BER versus \(\sigma\) and BER versus \(\frac{a_1-a_2}{2\sigma}\) curves and compare them with theory.

Part 4 deliverables

For this section, the deliverables are:

the answer to two deliverable questions,
the code used to generate the BER curves (with the datasets hard coded into it),
the resulting BER curves as a .PNG image file.

Generating a BER curve

Using the values collected throughout this lab you can now generate a BER curves.

You can use a programming language of your choice, but python and matlab have some handy tools for this job built in.

Plot two curves on the same axes:

BER curve for the theoretical \(BER=Q\left( \frac{a_1 - a_2}{2\sigma_0} \right)\),
BER curve using the collected BER and set \(\sigma\) values from earlier in this lab.

1. Theory

For generating a simulated curve of the theoretical BER versus \(\frac{a_1 - a_2}{2\sigma_0}\) review the theory section of this lab.

For the Q-function, Matlab ships with qfunc() while python has norm.sf() included in the scipy package.

Remember to plot two curves, one for bipolar (\(a_1, a_2 = 1, -1\)) and one for unipolar (\(a_1, a_2 = 1, 0\)). You can use the same \(\sigma\) values as those set during the experiment to ensure the curves will line up in the x-axis.

2. Collected BER and set \(\sigma\) values

You collected a dataset of BER values for \(\sigma\) values of [ 0.3, 0.5, 1, 1.5, 2, 3, 4, 5, 8, 12]. While plotting these remember that the BER values collected from the number sink are log10(BER). So to obtain the BER you will need to raise your collected values(-X) by realizing that \(BER = 10^{-X}\).

Plotting details

Now that you have the two curves, ensure that the plot has:

a log scale for \(\sigma\)
appropriate axes titles
a legend (one entry for each of: “unipolar sim.”, “unipolar theory”, “bipolar sim.”, “bipolar theory”)

Plot again but with BER as a function of \(\frac{a_1-a_2}{2\sigma}\). Ensure that this plot has:

a log scale for \(\frac{a_1-a_2}{2\sigma}\)
appropriate axes titles
a legend (one entry for each of: “unipolar sim.”, “unipolar theory”, “bipolar sim.”, “bipolar theory”)

A sample of what the plots might look like is included below (with labelling elements removed).

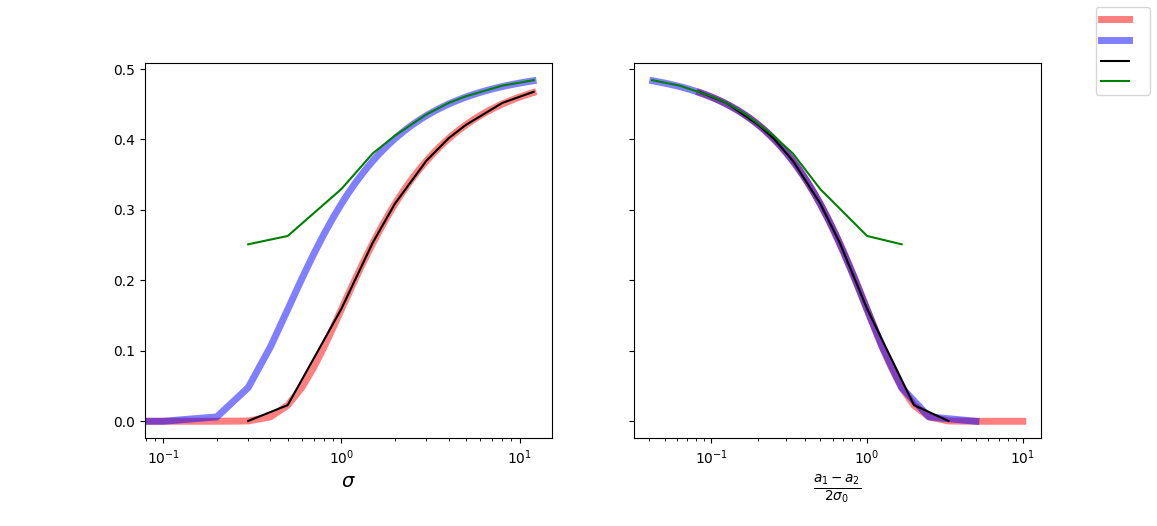
Sample BER curve

Deliverable question 3

Provide insight into your results. What does the BER curve tell you about each (unipolar/bipolar) communication system? What does it tell you about the performance of the two systems when compared?

Deliverable question 4

Discuss the differences between the two plots. Which is more useful in considering the performance of your communication system?

Review the section deliverables beforing moving on.