Part 3 - RRC pulse shaping

Objectives

You will implement a communications system using a Root Raised Cosine (RRC) filter for pulse shaping.

Part 3 deliverables

For this section, the deliverables are:

the answers to two deliverable questions,
a dataset for later use in this lab.

RRC pulse shaping flowgraph

Construct the following GRC flowgraph. It is very similar to the previous pulse shaping flowgraphs. You can “File>Save As” in GRC in order to not begin from scratch again.

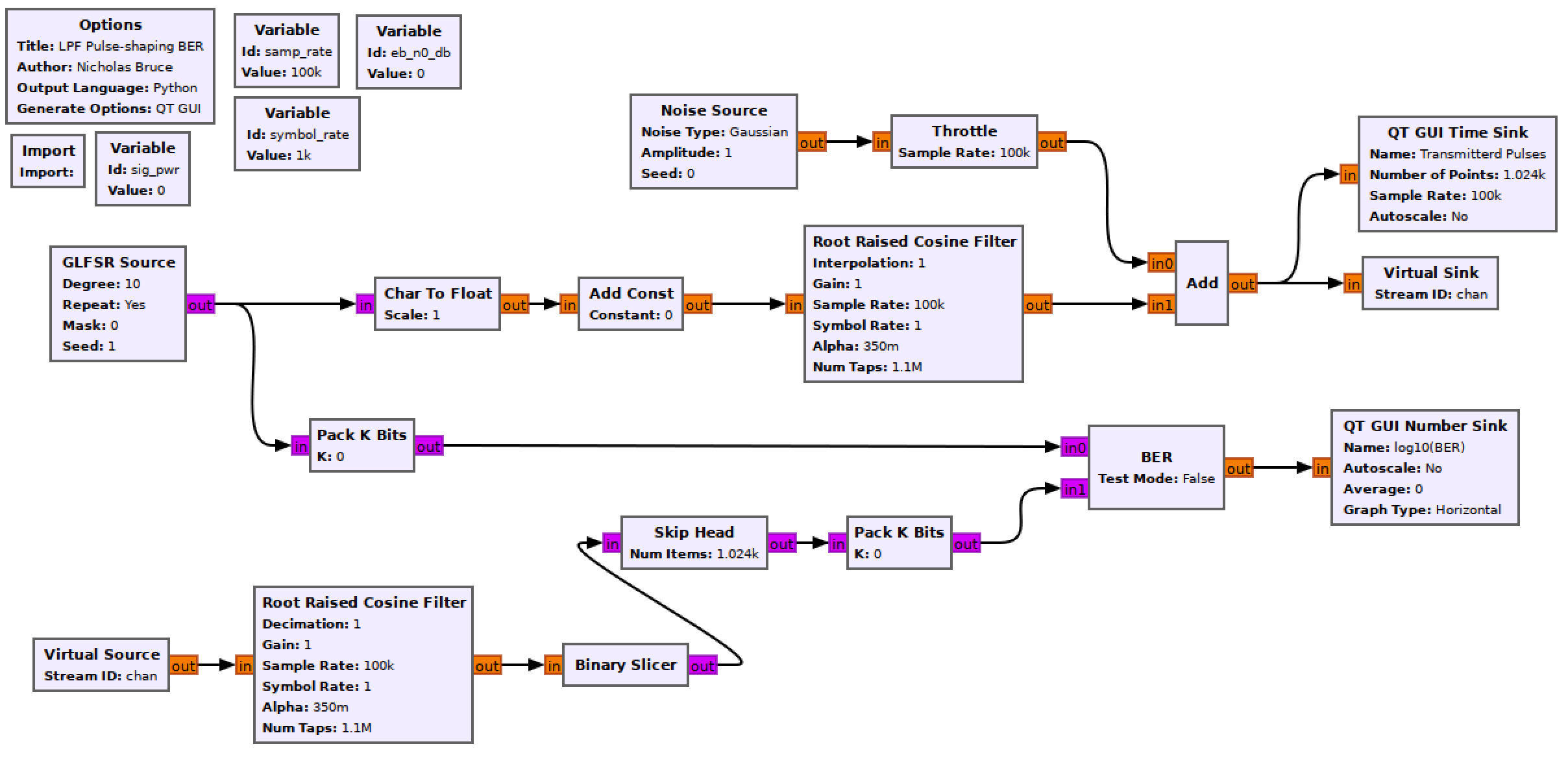
Blank RRC pulse shaping flowgraph

Variables

Replace the sigma variable with an eb_n0_db variable and set the value to 0.
Leave the sig_pwr variable blank for now.

Note

GR version 3.8.0.0 on windows might cause problems if you don’t cast the value to a float().

Import

The argument is import math. This will load the python math library. To call the library functions you would precede them with math. For example, to take the square root of the number 5 you would write math.sqrt(5) wherever you wanted the result.

Root Raised Cosine Filter (Transmitting)

The tranmitter chain is now pulse shaping with a Root Raised Cosine Filter block. Some parameters for the filter are

the filter is of type “Float->Float (Interpolating)”,
the filter roll-off factor (\(\alpha\)) indirectly specifies the bandwidth of the filter. Set \(\alpha=0.35\).
An ideal RRC filter has an infinite number of taps but in practice must be windowed. Set the number of taps to the sampling rate.
The symbol rate is the same as it was in the last lab section,
The interpolation factor is the same as for the previous pulse-shaping method (and for all pulse shaping methods it is the number of samples per symbol when coming from a bit stream to a waveform).
The gain can be found in the same way as with the LPF pulse shaping. Measure the amplitude and set the gain such that the peak of the shaped pulses are at about 1.

Root Raised Cosine Filter (Receiving)

The receiver chain is now using a matching Root Raised Cosine Filter to obtain a final pulse shape that is a raised cosine (review the theory section for more on this).

The filter is of type “Float->Float (Decimating)”
Set the number of taps to the sampling rate.
Set the symbol rate and decimation rates appropriately.
Do not change the gain, by observing the output of the filter you will see that the input symbols (scaled to 1 above) are all either 1 or -1.

Note

Since this is a matched filter it is the dual to the transmitter RRC filter. Its parameters should reflect this.

Deliverable question 2

Consider the time domain shape (impulse response) of the root raised cosine filter. In an ideal system, RRC filters have zero-ISI (inter-symbol interference). Why is this? It may help your understanding to draw multiple pulses [1, 1, 1] next to each other.

Skip Head

The offset between sequences can be found as before. It is 1000 samples with the above listed filter parameters (which means a 500 sample delay for each component of the matched filter).

Validate the filter

Ensure that the offset and matched filter are working by setting the Amplitude of the Noise Source block to 0 and checking that the BER is 0.

Finding the signal power

In order to control the simulation, we need to set the eb_n0_db variable and have that control the noise power (\(\sigma\)) in the Noise Source block. This can be done using the equation you derived in the prelab. In translating the equation into a line of python (so that it can be used in GNU Radio), see that \(f_{SYM}\) is symbol_rate and \(f_s\) is samp_rate.

In this equation, \(a_i^2\) is the signal power. This is the only parameter still unknown. Build the following three blocks to measure the signal power and attach the output of the transmitting RRC to both inputs of the multiply block.

Flow diagram to measure average power of a data stream.

The Length of the Moving Average block is 100000 and the Scale is the inverse (ensure that the inverse is a float and not an integer.)

Note

Ensure that the Scale parameter is a float and not an integer. GR versions < 3.8 are build on Python 2 and so 1/100000 will result in the int 0. GR versions 3.8+ are built on Python 3 and so the same argument will yield the float 0.00001. In GR versions < 3.8 this can be solved by casting the entire argument as a float by wrapping it with a float().

Run the flowgraph and record this power value. Take a second and consider whether the value you have measured is reasonable. The peaks of the RRC output are at about 1 after the gain adjustment above. Save the measured value in the sig_pwr variable block.

Now all of the variables in the above derivation for \(\sigma\) have been found. It is now possible to control the \(\frac{E_b}{N_0} \text{ (dB)}\) of the system by holding the signal power constant and varying the noise power. Enter the expression for \(\sigma\) in the Amplitude parameter of the Noise Source block. It should be a function of samp_rate, symbol_rate, sig_pwr, and eb_n0_db.

Running the experiment

Run the flowgraph. Record the BER at \(\frac{E_b}{N_0}\) values of 0, 2, 4, 6, 8 dB.
- Plotting the time sink values also eats computational power. You may disable the QT GUI Time Sink blocks and any other unneeded QT GUI blocks.
- * Ensure that when you change the eb_n0_db variable value that the Amplitude of the Noise Source also changes. If sigma is not changing something is wrong (if you’re on windows, you might be able to wrap the eb_n0_db variable in a float() cast. *
Offset the delay (in the Skip Head block) by a single sample. Check the BER with no added noise.
When discussing an Eb/N0 value, it refers to the received energy per bit/noise power ratio. The \(\sigma\) formula above is true for a matched filter as it relies on the input signal power and is true for WGN. What if this simulation was not a MF and not WGN? The standard method of calculating Eb/N0 would be to measure the output signal and noise powers as done in the previous section of the lab. Conduct the appropriate measurements to find the Eb/N0 value independent of input signal or noise powers.
- Add the Multiply->Moving Average->QT GUI Number Sink power measuring chain to the output of the receiving RRC filter. Record a power measurement there for:
  - Signal power (set noise power to 0).
  - Noise powers required for Eb/N0 of 0, 2, 4, 6, 8 dB (to do this, set the Gain in the Transmitting RRC to 0)

Deliverable question 3

Consider the relative impact of noise versus a timing offset on the system. Does the RRC filter fare any better than the LPF did with an offset of 1 sample?

From this section you should have recorded 5 BER values, 5 output noise power values and 1 output signal power value.

Review the section deliverables beforing moving on.