Part 4 - Coherent FSK

Objectives

You will implement a coherent real passband FSK receiver to demodulate the transmitting signal chain previously built.

Part 4 deliverables

For this section, the deliverables are:

the answers to two deliverable questions,
a dataset for later use in this lab.

Building the flowgraph

Construct the following GRC flowgraph. You can make a copy of the modulating flowgraph from the last section as a starting point by “Save As”-ing it.

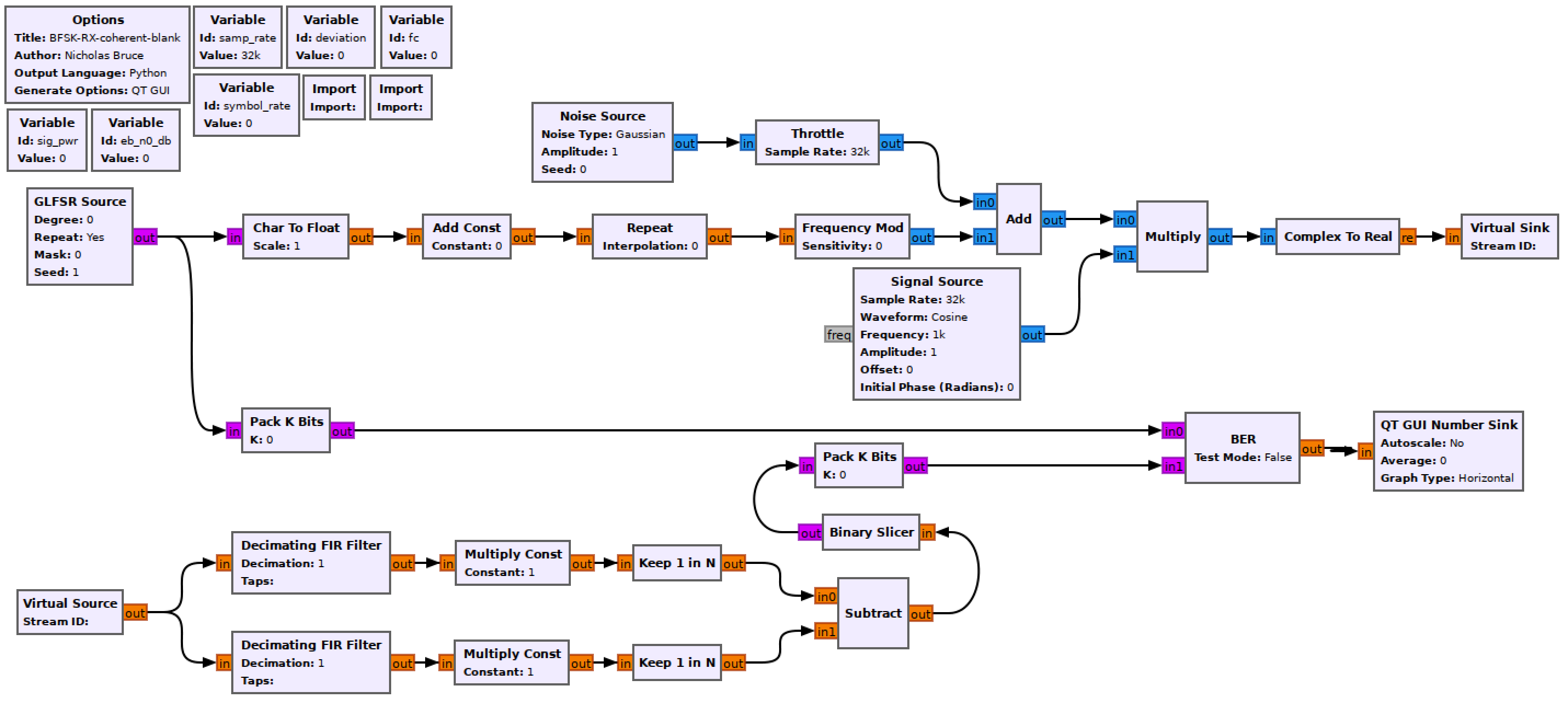
Coherent BFSK simulation flowgraph.

Variables

Add a Variable block called fc set to 1800. This will be the center frequency of the transmitted real signal.

Set \(f_s\) to 76800 Hz. Keep \(f_{sym}\) at 1200 Hz and set \(f_{dev}\) to \(\frac{f_{sym}}{2}\).

Import

Use a second Import block to import NumPy, a common scientific computing package for Python. Import it using the following expression.

import numpy as np

This syntax allows you to use the the package functions by calling np.package_name instead of typing out numpy.package_name.

Modulator

The modulator is the same as in the previous section with the addition of a complex multiplier to raise the baseband signal to a passband BFSK signal centered around fc. The real part of the signal is then taken and transmitted.

Noise Source

The amplitude (standard deviation) of the noise source is very close to the same as before but with a factor of 0.5 multiplied in.

\[\begin{align} \frac{E_b}{N_0} &= \frac{a_i^2}{\sigma_0^2}\frac{W}{R} = \frac{a_i^2}{\sigma_0^2}\frac{f_s}{f_{sym}} \text{(Complex baseband)} \\ \frac{E_b}{N_0} &= \frac{a_i^2}{\sigma_0^2}\frac{W}{R} = \frac{1}{2}\frac{a_i^2}{\sigma_0^2}\frac{f_s}{f_{sym}} \text{(Real passband)} \\ \end{align}\]

Deliverable question 4

Why does the real passband expression for \(\frac{E_b}{N_0}\) have a factor of 0.5 that does not exist in the complex baseband?

Set the amplitude parameter to the following expression.

math.sqrt( sig_pwr/ (10**(eb_n0_db/10)) * samp_rate/symbol_rate * 1/2 )

This is the same expression as from the above theory but where \(\frac{E_b}{N_0}\) is in units of dB.

Receiver chain

This is a coherent receiver which is built based on Sklar text section 4.4.4.

Decimating FIR Filter

Each of these is a matched filter for a single symbol period of one of the two passband frequencies, \(f_c \pm f_{dev}\).

Set the taps in the upper path to the following expression.

np.cos(2*np.pi*(fc+deviation)*np.arange(0, symbol_rate**-1, samp_rate**-1))

Set the taps in the lower path to the following expression.

np.cos(2*np.pi*(fc-deviation)*np.arange(0, symbol_rate**-1, samp_rate**-1))

The expressions are plotted below.

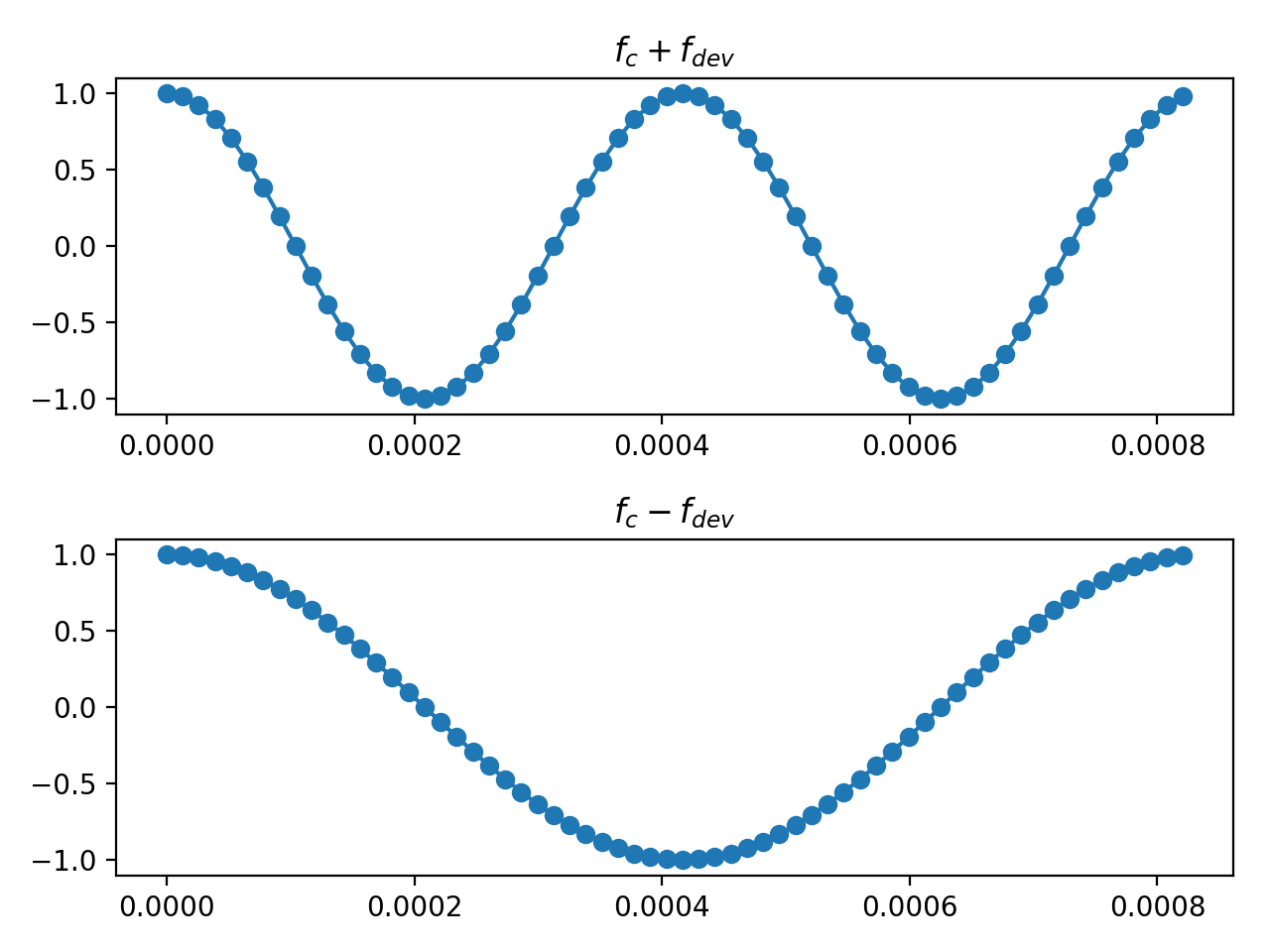
Taps for the two matched filters.

Multiply Const

Following the theory in Sklar text section 4.4.4, the waveform can be normalized by the factor \(\sqrt{\frac{2}{T}}\). Implement this factor using the available variables (it will be one over this number).

Keep 1 in N

Use these blocks to sample the output of the matched filters on the peaks of the waveform. The argument is the decimation rate. This also decimates the sample rate down to the GLFSR rate of one-sample-per-symbol.

Binary Slicer

This block outputs a 0 for every negative input and a 1 for every positive output.

Pack K Bits

Set K to 8. This is the packet byte size that the later BER block requires.

BER

This computes the error between the two inputs. It outputs to log of the BER, so if it outputs a value of -2, the BER is \(10^{-2}=0.01\).

Set Test Mode to False, which will mean the block immediately starts outputting results (as opposed to waiting for the error rate to stabilize first). While Test Mode is False, the other parameters don’t do anything, so you can leave them as they are.

QT GUI Number Sink

This will draw the output of the BER block on a number line. Set the maximum to 0 (since \(10^0=1\) meaning that every bit is wrong) and the minumum to -7.

Analysing the receiver

To understand the demodulation it is important to view the waveform at various steps. First observe the transmitted waveform.

Place a QT GUI Time Sink with 2 “Float” inputs near the end of the receiver chain. Connect the outputs of the Repeat and Complex To Real blocks to the sink.
Put a 0* in front of the Noise Source’s expression for \(\sigma\) so that there is no noise in the waveform.
Run the flowgraph and observe.

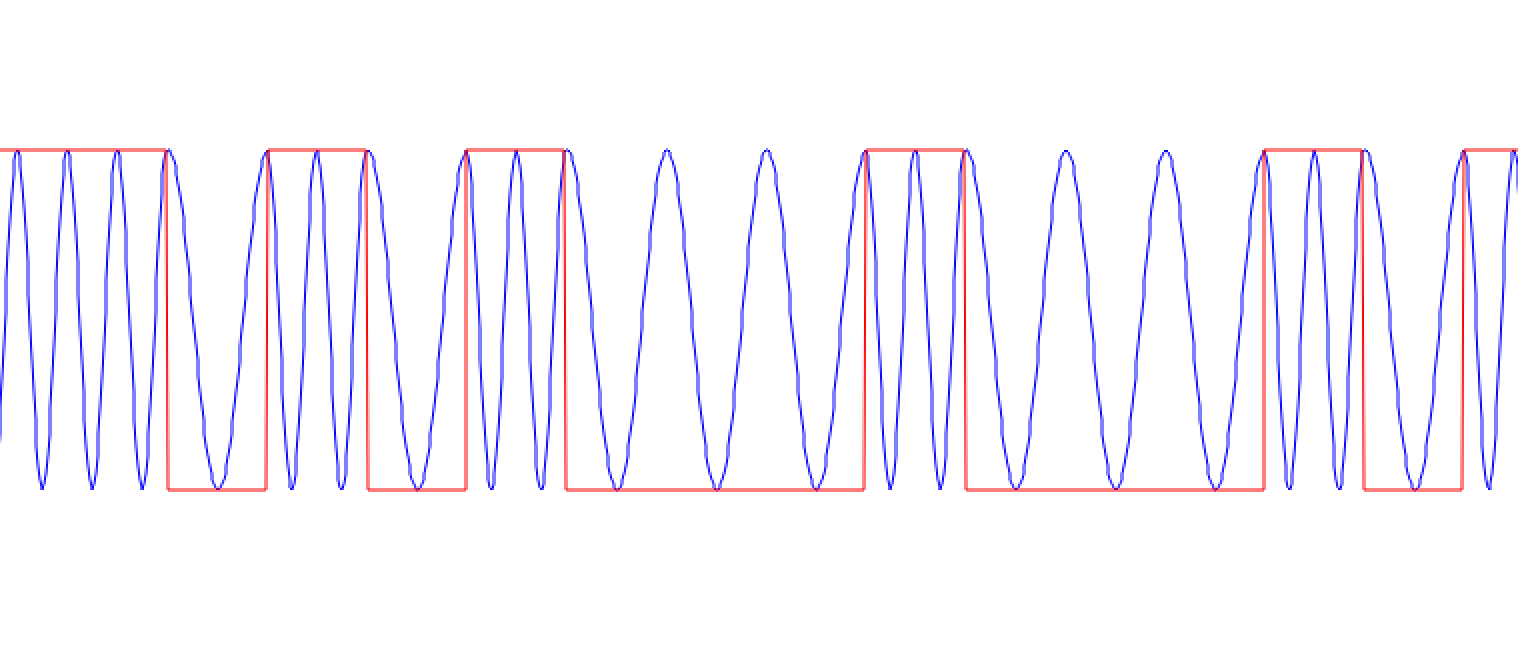
Transmitted passband waveform.

The two distinct frequencies (1200 Hz and 2400 Hz) can seen clearly. One correlates with an input bit of -1 while the other correlates with an input bit of 1. When a single 1 or -1 is transmitted the waveform matches the taps which were shown earlier. When the bit repeats ([1, 1, 1, ...] or [-1, -1, -1, ...]) the waveform continues at that frequency until the bit value changes.

Now observe various stages of the receiver.

Increase the number of inputs to the QT GUI Time Sink to 3. Connect the outputs of the two matched filters (after scaling) as well as the output of the Repeat block.

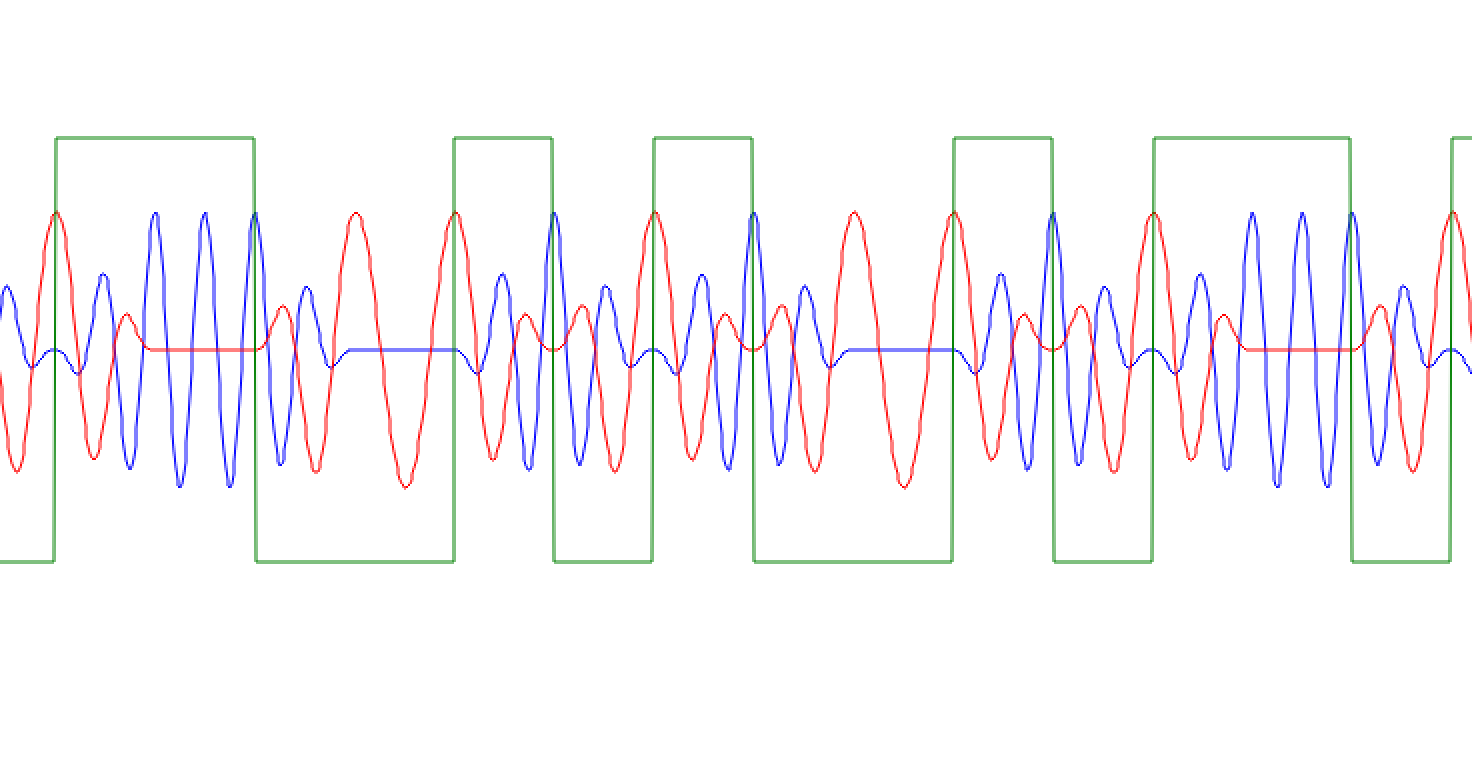
Output of the matched filters.

Notice the delay caused by the FIR filters between the filter outputs and the square waveform. It can be removed by delaying the square waveform at the input of the Sink by the number of filter taps (\(M\), where this is an M-sample-per-symbol square wave). More importantly, notice that the waveforms coming out of the matched filter flip. One exists while the other is zero. It is no stretch to imagine these as 1’s and 0’s (amplitude “ons” and amplitude “offs”).

Disable the QT GUI Time Sink and add a new one with 1 “Float” inputs. View the outputs of the Keep 1-in-N blocks. These blocks sample the waveform peaks.

Decimated output of the matched filters.

Notice that in this noiseless system, the two signals are redundant. The same performance would be obtained by only observing the output of a single matched filter.

Deliverable Question 5

Once noise is added, imagine a situation where the decimated output of one MF stream is near to but not exactly zero. What do you expect at the output of the other decimated MF?

Disable all of the QT GUI Time Sink blocks. Remove the 0* from the Noise Source \(\sigma\) parmeter.

Run the experiment

Run the flowgraph.
Record the BER at \(\frac{E_b}{N_0}\) values of [0, 2, 4, 6, 8, 10]. You will need to kill the flowgraph each time you need to set a new value.
- Plotting GUI sink values also eats computational power. While waiting for the BER values to stabilize you may wish to disable any unneeded QT GUI blocks.

At this point you should have recorded 6 BER values.

Review the section deliverables before moving on.