Part 2 - FSK Modulator

Edit me

Objectives

You will build and study a complex baseband FSK modulator.

Part 2 deliverables

For this section, the deliverables are:

the answer to two deliverable questions,
a flowgraph to reuse later in the lab.

Building the flowgraph

Construct the following GRC flowgraph.

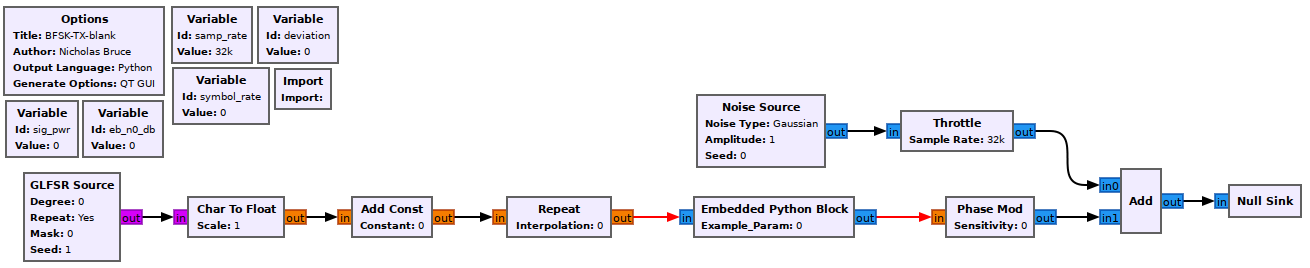
Blank BFSK modulator flowgraph

Variables

The samp_rate of this flowgraph is 76.8 kHz and the symbol_rate is 1200 Hz.
Set the deviation variable appropriately for a noncoherent receiver (review the theory section if needed).
Leave the other variables set to 0 for now.

Import

Import the math library with import math.

GLFSR Source

This block outputs a pseudo-random bit stream using a shift register as described in the theory section of Lab 1. Set the Degree of the shift register to 20 (this is the LFSR’s \(M\) value). Set it to repeat.

Char To Float & Add Const

The output of the GLFSR block is a series of 1’s and 0’s. In order to build a bipolar signal the 0s must become -1s. This can be done using the following equation

\[y[n] = 2x[n]-1\]

where \(y[n]\) is the output stream made up of -1s and 1s and \(x[n]\) is the input stream of 0s and 1s.

Setting the Scale parameter of the Char To Float block to 0.5 and the Constant parameter of the Add Const block to -1. You can observe the output of the Add Const block using a QT GUI Constellation Sink to see that this is now a bipolar signal.

Repeat

Now use the repeat block to turn the 1-sample-per-symbol signal into an M-sample-per-symbol square pulse-shaped signal. Use the samp_rate and symbol_rate variables.

Embedded Python Block

This block allows you to create a custom block by writing some Python and embedding it in the flowgraph. Recalling the expression for a sampled complex baseband BFSK signal, the output of the Repeat block is \(m(\alpha)\). This Embedded Python Block will be made into a cumulative sum block so that the output of the block is the integral, \(\int_0^t m(\alpha)d\alpha\).

Open the block and click “Open in Editor”. You will now be able to edit the Python that processes the input. The code already filling the block takes the input and multiplies it by a constant, delivering the product as the blocks output. First look at the constructor (__def init()__). It takes an argument and a default value for it, example_param=1.0. Anything added here becomes a parameter of the block which can be easily adjusted from the normal block parameters GUI. Since the cumulative sum requires no input paramters, remove the argument.

A few lines lower is the name of the block, name='Embedded Python Block'. You can change it to something more meaningful, like CumSum so that the flowgraph is easy to interpret. The next two lines indicate the input and output signal types. The default is np.complex64. Looking back at the flowgraph you can see that the necessary datatype is a float (np.float32) so change them appropriately.

The callback slightly lower is for the example paramter and it can be removed since the example_param argument no longer exists. We will now add a variable to store the cumulative sum. Add the following line where the callback used to be.

self.cumsum = [0.0]

Now the work() function must be changed. Reading through it now shows the multiplication with the example parameter. Remove this and replace it with the following:

for i in np.arange(len(output_items[0])):
  self.cumsum += input_items[0][i]
  out_items[0][i] = self.cumsum

return len(output_items[0])

The input to the block is delivered in chunks of samples (the size of the chunk depends on a number of factors including OS and available hardware, but is generally around 8192 samples). This code block will take the input, add every input to the existing cumulative sum and put it in the output buffer. The complete code snippet should look like the following.

"""
Embedded Python Blocks:

Each time this file is saved, GRC will instantiate the first class it finds
to get ports and parameters of your block. The arguments to __init__  will
be the parameters. All of them are required to have default values!
"""

import numpy as np
from gnuradio import gr


class blk(gr.sync_block):
    """Embedded Python Block - Cumulative Sum"""

    def __init__(self):
        gr.sync_block.__init__(
            self,
            name='CumSum',       # will show up in GRC
            in_sig=[np.float32], # input datatype
            out_sig=[np.float32] # output datatype
        )
        self.cumsum = [0.0]


    def work(self, input_items, output_items):
        in_arr = input_items[0]
        out_arr = output_items[0]

        for i in np.arange(len(output_items[0])):
            self.cumsum += input_items[0][i]
            output_items[0][i] = self.cumsum

        return len(output_items[0])

Save your changes and exit back to the flowgraph.

Phase Mod

It is helpful to see the Phase Mod documentation. This block has one parameter, Sensitivity and the output is \(e^{j*sensitivity*input}\). Recall from the theory section that

\[\tilde{s}(t) = e^{\frac{j2\pi f_{dev}}{f_s} \int^t_0 m(\alpha)d\alpha}.\]

Set the Sensitivity of the block to 2*math.pi*deviation/samp_rate so that the output of the block is \(\tilde{s}(t)\).

Noise Source

For now leave it with default parameters.

Run the experiment

Add a QT GUI Time Sink to the flowgraph. Set the Type to Float and the Number of Inputs to 4. You can use the Config tab to label the 4 inputs as m_alpha, int_m_alpha, Re(s~(t)) and Im(s~(t)). Connect the respective inputs to the output of the Repeat, CumSum, and Phase Mod blocks (you’ll need a Complex To Float block to connect the output of the Phase Mod).

Don’t forget to activate the the Control Panel in the block!

The ramp coming out of the CumSum block will rise and fall by much greater than the maximum value of 1 (as shown in the theory section of this lab that the other outputs have. To “wrap” the ramp (much like phase wrapping), add another Python Block in between the output of the CumSum block and the input of the QT GUI Time Sink block. This is done solely to keep the phase ramp within easy-to-read bounds that match the limits of the waveform amplitude. Replace the code in the block with the following segment

import numpy as np
from gnuradio import gr


class blk(gr.sync_block):
  """Embedded Python Block that wraps the input given some bounds"""

  def __init__(self, sample_rate=0.0, symbol_rate=0.0, low=-1.0, high=1.0):  # only default arguments here
      """arguments to this function show up as parameters in GRC"""
      gr.sync_block.__init__(
          self,
          name='Wrap',
          in_sig=[np.float32],
          out_sig=[np.float32]
      )
      # callbacks
      self.samp_rate = sample_rate
      self.symbol_rate = symbol_rate
      self.low = low
      self.high = high

  def bound(self, value):
      """Wraps and normalizes input"""
      value = value/(self.samp_rate/self.symbol_rate)
      diff = self.high-self.low
      return (((value-self.low) % diff) + self.low)

  def work(self, input_items, output_items):
      for i in np.arange(len(output_items[0])):
          output_items[0][i] = self.bound(input_items[0][i])

      return len(output_items[0])

Now you can open the block like any other and set the “Low” and “High” parameters to whatever you want. It should default to -1 and 1 respectively which is appropriate for this scenario.

Run the flowgraph. Stop it soon after starting so that the plot freezes. You should see a figure like the following
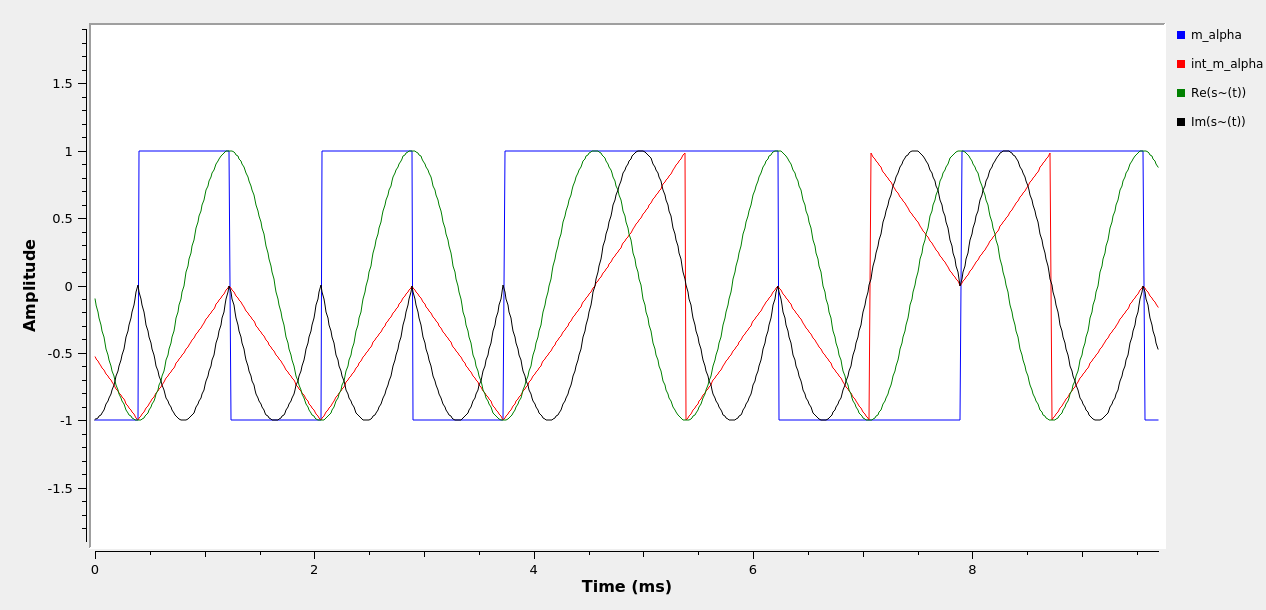
\(m(\alpha), \int_0^t m(\alpha) d\alpha, \mathbb{Re}\left\{\tilde{s}(t)\right\}, \mathbb{Im}\left\{\tilde{s}(t)\right\}\) plotted together in GNU Radio.
If you wish to see the signal at passband, multiply the signal coming out of the Phase Mod block with a complex cosine with a frequency of 1500 Hz.

Deliverable question 1

In the figure above (and the simulation!) where \(m(\alpha)\) changes value, it is clear that \(\int_0^t m(\alpha)d\alpha\) changes direction and \(\mathbb{Im}\left\{ \tilde{s}(t) \right\}\) obviously changes as well. Why does \(\mathbb{Re}\left\{ \tilde{s}(t) \right\}\) not appear to change?

Deliverable question 2

In the figure above (and the simulation!) where \(\int_0^t m(\alpha) d\alpha\) has two distinct ‘peak types’. One is a sawtooth (an equal but opposite slope on each side) while the other is sharper (a slope on one side but vertical on the other). What is the difference?

Review the section deliverables before moving on.